| 八毛小说网 玄幻小说 武侠小说 仙侠小说 都市小说 言情小说 校园小说 历史小说 军事小说 网游小说 竞技小说 穿越小说 重生小说 |
| 小说排行榜 官场小说 架空小说 耽美小说 科幻小说 灵异小说 推理小说 同人小说 经典名著 乡村小说 短篇文学 综合其它 总裁小说 |
| 好看的小说 女人如烟 一世之尊 罪恶之城 孽乱村医 绝世武神 我欲封天 小姨多春 完美世界 神武八荒 官路红颜 全本小说 热门小说 |
|
《金史》卷三及《金史》最新章节在线阅读
|
|
|
|
| 八毛小说网 > 历史小说 > 金史 作者:脱脱等 | 书号:10206 时间:2017/3/26 字数:14782 |
| 上一章 卷三 下一章 ( → ) | |
| ◎历下 ○步月离第五 转终分：一十四万四千一百一十，秒六千六十六。 转终⽇：二十七⽇，余二千九百，秒六千六十六。 转中⽇：一十三⽇，余四千六十五，秒三千三十三。 朔差⽇：一，余五千一百四，秒三千九百三十四。 象策：七⽇，余二千一分，二十二秒半。 秒⺟：一万。 上弦：九十一度，三十一分，四十二秒。 望：一百八十二度，六十二分，八十四秒。 下弦：二百七十三度，九十四分，二十六秒。 月平行度：十三度，三十六分，八十七秒半。 分、秒⺟：一百。 七⽇：初数，四千六百四十八。末数，五百八十二。 十四⽇：初数，四千六十五。末数，一千一百六十五。 二十一⽇：初数，三千四百八十三。末数，一千七百四十七。 二十八⽇：初数，二千九百一。末数，二千三百二十九。 求经朔弦望⼊转 置天正朔积分，以转终分及秒去之，不尽，如⽇法而一，为⽇，不満为余秒，即天正十一经月朔⼊转⽇及余秒。以象策累加之，去命如前，即得弦、望经⽇加时⼊转⽇及余秒。径求次朔⼊转。(以朔差加之。) 转定分及积度朓棵率 (表略) 求朔弦望⼊转朓棵定数 置⼊转小余，以其⽇算外，损益率乘之，如⽇法而一，所得，以损益积为定数。其四七⽇下余，如初数以下，初率乘之，初数而一，以损益朓棵积为定数。如初数以上，初数减之，余乘末率，末数而一，便为朓棵定数。 求朔弦望定⽇ 置经朔、弦、望小余，朓减朒加⼊气⼊转朓棵定数，満与不⾜，进退大余，命甲子算外，各得定朔、弦、望⽇辰及余。定朔前⼲名与后⼲名同者，其月大；不同者，其月小。月內无中气者为闰。视定朔小余：秋分后，在⽇法四分之三以上者，进一⽇。舂分后，定朔⽇出分与舂分⽇出分相减之余，三约之，用减四分之三，定朔小余及此数以上者，亦进一⽇。或有  ，亏初在⽇⼊前者，不进之。定弦、望小余在⽇出分以下者，退一⽇。望或有 ，亏初在⽇出前者，小余虽在⽇出后，亦退之。如十七⽇望者，又视定朔小余在四分之三以下之数，(舂分后用减定之数。)与定望小余在⽇出分以上之数相较之；朔少望多者，望不退，而朔犹进之。望少朔多者，朔不进，而望犹退之。(⽇月之行，有盈有缩，迟疾加减之数，或有四大三小；若随常理，当察其时早晚，随所近而进退之，使不过三大二小。)求定朔弦望中积 置定朔、弦、望大小余与经朔、弦、望大小余相减之余，以加减经朔、弦、望⼊气⽇余，(经朔、弦、望少即加之，多即减之。)即为定朔、弦、望⼊气。以加其气中积，即为定朔、弦、望中积。(其余以⽇法退除为分秒。) 求定朔弦望加时⽇度 置定朔、弦、望约余，以所⼊气⽇损益率乘，(盈缩损益。)万约之，以损益其下盈缩积，乃盈加缩减定朔弦望中积；又以冬至加时⽇躔⻩道宿度加之，依宿次去之，即得定朔、弦、望加时⽇所在度及分秒。又置定朔、弦、望约余，副置之。以乘其⽇盈缩之损益率，万约之，应益者盈加缩减，应损者盈减缩加其副，満百为分，分満百为度，以加其⽇夜半⽇度，命之，各得其⽇加时⽇躔⻩道宿次。(若先于历注定每⽇夜半⽇度，即为妙也。) 求定朔弦望加时月度 凡合朔加时⽇月同度，其定朔加时⻩道⽇度，即为定朔加时⻩道月度。弦、望各以弦、望度加定弦、望加时⻩道⽇度，依宿次去之，即得定朔、弦、望加时⻩道月度及分秒。 求夜半午中⼊转 置经朔⼊转，以经朔小余减之，为经朔夜半⼊转。又经朔小余与半法相减之余，以加减经朔加时⼊转，(经朔少，如半法加之；多，如半法减之。)为经朔午中⼊转。若定朔大余有进退者，亦加减转⼊，否则因经为定。每月累加一⽇，満终⽇及余秒去命如前，各得每⽇夜半、午中⼊转。(求夜半，因定朔夜半⼊转累加之。求午中，因定朔午中⼊转累加之。求加时⼊转者，如求加时⼊气术。) 求加时及夜半月度 置其⽇⼊转算外转定分，以定朔、弦、望小余乘之，如⽇法而一，为加时转分。(分満百为度。)减定朔、弦、望加时月度，为夜半月度。以所得转定分累加之，即得每⽇夜半月度。(或朔至弦、望，或至后朔，皆可累加之。然近则差少，远则差多。置所求前后夜半相距月度为行度，计其相距⼊转积度，与行度相减，余以相距⽇数除为⽇差，行度多以⽇差加每⽇转定分，行度少以⽇差减每⽇转定分，然后用之可中。或  速求，用此数，究其故，宜用后术。)求晨昏月度 置其⽇晨分，乘其⽇算外转定分，⽇法而一，为晨转分。用减定分，余为昏转分。又以朔、弦、望定小余、乘转定分，⽇法而一，为加时分。以减晨、昏转分，为前；不⾜，覆减之，为后。乃前加后减加时月度，即晨昏月所在宿度及分秒。 求朔弦望晨昏定程 各以其朔昏定月，减上弦昏定月，余为朔后昏定程。以上弦昏定月，减望昏定，余为上弦后昏定程。以望晨定月，减下弦晨定月，余为望后晨定程。以下弦晨定月，减后朔晨定月，余为下弦后晨定程。 求每⽇转定度 累计每程相距⽇下转积度，与晨昏定程相减，余以相距⽇数除之，为⽇差，(定程多加之，定程少减之。)以加减每⽇转定分，为转定度。因朔、弦、望晨昏月，每⽇累加之，満宿次去之，为每⽇晨昏月度及分秒。(凡注历：朔⽇以后注昏月，望后一⽇注晨月。)古历有九道月度，其数虽繁，亦难削去，具其术如后。 求平 ⽇辰置 终⽇及余秒，以其经月朔加时⼊泛⽇及余秒减之，为平⼊其经月朔加时后⽇及余秒。以加其经月朔大小余，其大余命甲子算外，即平⽇辰及余秒。(求次者，以终⽇及余秒加之，大余満纪法去之，命如前，即次平⽇辰及余秒。)求平 ⼊转朓棵定数置平 小余，加其⽇夜半⼊转余，以乘其⽇损益率，⽇法而一，所得，以损益其下朓朒积，为定数。求正 ⽇辰置平 小余，以平⼊转朓棵定数，朓减朒加之，満与不⾜，进退⽇辰，即正⽇辰及余秒。与定朔⽇辰相距，即所在月⽇。求经朔加时中积 各以其经月朔加⼊气⽇及余，加其气中积余，其⽇命为度，其余以⽇法退除为分秒，即其经朔加时中积度及分秒。 求正 加时⻩道月度置平 ⼊经朔加时后算及余秒，以⽇法通⽇，內余，进二位，如三万九千一百二十一分为度，不満退除为分秒，以加其经月朔加时中积，然后以冬至加时⻩道⽇度加而命之，即其得其月正加时月离⻩道宿度及分秒。如求次者，以终度及秒加而命之，即得所求。求⻩道宿积度 置正 时⻩道宿全度，以正加时月离⻩道宿度及分秒减之，余为距后度及分秒，以⻩道宿度累加之，即各得正后⻩道宿积度及分秒。求⻩道宿积度⼊初末限 置⻩道宿积度及分秒，満 象度及分秒去之，如在半象以下，为初限；以上者，以减象度及分秒，余为⼊末限。(⼊积度象度并在会术中。)求月行九道宿度 凡月行所 ：冬⼊ 历，夏⼊ 历，月行青道。(冬至夏至后，青道半在舂分之宿，当⻩道东。立冬立夏后，青道半在立舂之宿，当⻩道东南。至所冲之宿亦如之。)冬⼊历，夏⼊历，月行⽩道。(冬至夏至后，⽩道半在秋分之宿，当⻩道西。立冬立夏后，⽩道半在立秋之宿，当⻩道西北。至所冲之宿亦如之。)舂⼊历，秋⼊历，月行朱道。(舂分秋分后，朱道半在夏至之宿，当⻩道南。立舂立秋后，朱道半在立夏之宿，当⻩道西南。至所冲之宿亦如之。)舂⼊历，秋⼊历，月行黑道。(舂分秋分后，黑道半在冬至之宿当⻩道北。立舂立秋后，黑道半在立冬之宿，当⻩道东北。至所冲之宿亦如之。)四序离为八节，至之所，皆与⻩道相会，故月行有九道。各以所⼊初末限度及分秒，减一百一度，余以所⼊初末限度及分乘之，半而退位为分，分満百为度，命为月道与⻩道泛差。凡⽇以⾚道內为，外为；月以⻩道內为，外为。故月行正，⼊夏至后宿度內为同名，⼊冬至后宿度內为异名。其在同名者，置月行与⻩道泛差，九因八约之，为定差，半后，正前，以差减；正后，半前，以差加。(此加减出⼊六度，正，如⻩⾚道相同名之差，若较之渐异，则随所在，迁变不同也。)仍以正度距秋分度数，乘定差，如象限而一，所得为月道与⾚道定差。前加者为减，减者为加。其中异名者，置月行与⻩道泛差，七因八约之，为定差。半后，以差加；正后，半前，以差减。(此加减出⼊六度，异，如⻩道⾚道相异名之差，较之渐同，则随所迁变不常。)仍以正度距舂分度数，乘定差，如象限而一，所得为月道与⾚道定差。前加者为减，减者为加。各加减⻩道宿积度，为九道宿积度。以前宿九道积度减之，为其宿九道度及分。(其分就近约为太半少。论舂夏秋冬以四时⽇所在宿度为正。)求正 加时月离九道宿度以正 加时⻩道⽇度及分，减一百一度，余以正度及分乘之，半而退位为分，分満百为度，命为月道与⻩道泛差。其在同名者，置月行与⻩道泛差。九因八约之，为定差，以加；仍以正度距秋分度数，乘定差，如象限而一，所得为月道与⾚道定差，以减，其在异名者，置月行与⻩道泛差，七因八约之，为定差，以减；仍以正度距舂分度数，乘定差，如象限而一，所得为月道与⾚道定差，以加。置正加时⻩道月度及分，以二差加减之，即为正加时月离九道宿度及分。求定朔望加时月所在度 置定朔加时⽇躔⻩道宿次，凡合朔加时，月行潜在⽇下，与太 同度，是为加时月离宿次。各以弦、望度及分秒，加其所当弦、望加时月躔⻩道宿度，満宿次去之，命如前，各得定朔、弦、望加时月所在⻩道宿度及分秒。求定朔弦望加时九道月度 各以朔、弦、望加时月离⻩道宿度及分秒，加前宿正 后⻩道积度，为定朔、弦、望加时正后⻩道积度。如前求九道积度，以前宿九道积度减之，余为定朔、弦、望加时九道月离宿度及分秒。(其合朔加时，若非正，则⽇在⻩道，月在九道，所⼊宿度，虽多少不同，考其两极，若应绳准。故云：月行潜在⽇下，与太同度，即为加时九道月度。其求晨昏夜半月度，并依前术。)步 会第六终分：一十四万二千三百一十九，秒九千三百六十八。终⽇：二十七⽇，余一千一百九分，秒九千三百六十八。中⽇：十三，余三千一百六十九，秋九千六百八十四。朔⽇：二，余一千六百六十五，秒六百三十二。望⽇：十四，余四千二，秒五千。秒⺟：一万。 终：三百六十三度，七十九分，三十六秒。中：一百八十一度，八十九分，六十八秒。象：九十度，九十四分，八十四秒。半 象：四十五度，四十七分，四十二秒。⽇蚀既前限：二千四百。定法：二百四十八。 ⽇蚀既后限：三千一百。定法：三百二十。 月蚀限：五千一百。 月蚀既限：一千七百。定法：三百四十。 分秒⺟：一百。 求朔望⼊ 置天正朔积分，以 终分去之，不尽，如⽇法而一，为⽇，不満为余，即天正十一经月朔加时⼊泛⽇及余秒。朔加之，得次朔。望加之，得次望。再加望，亦得次朔。各为朔、望⼊泛⽇及余秒求定朔每⽇夜半⼊ 各置⼊ 泛⽇及余秒，减去经朔、望小余，即为定朔、望夜半⼊泛⽇及余秒。若定朔、望有进退者，亦进退⽇，否则因经为定。大月加二⽇，小月加一⽇，余皆加四千一百二十秒六百三十二，即次朔夜半⼊。累加一⽇，満终⽇及余秒去之，即每⽇夜半⼊泛⽇及余秒。求定朔望加时⼊ 置经朔、望加时⼊ 泛⽇及余秒，以⼊气⼊转朓棵定数，朓减朒加之，即定朔加时⼊泛⽇及余秒。求定朔望加时⼊ 积度及历置定朔、望加时⼊ 泛⽇，以⽇法通之，內余，进二位，如三万九千一百二十一而一为度，不満退除为分秒，即定朔、望加时月行⼊积度。以定朔、望加时⼊转迟疾度，迟减疾加之，即月行之⼊定积度。如中度以下，⼊历积度；以上，去之，余为⼊历积度。(每⽇夜半，准此求之。)求月去⻩道度 视月⼊ 历积度及分，如象以下，为少象；以上，覆减中，余为老象。置所⼊老少象度于上，列象度于下，相减相乘，倍而退位为分，満百为度，用减所⼊老少象度及分，余又与中度相减相乘，八因之，以百一十除为分，分満百为度，即得月去⻩道度。求朔望加时⼊ 常⽇及定⽇朔望⼊ 泛⽇，以⼊气朓棵定数，朓减朒加之，为⼊常⽇。又置⼊转朓棵定数，进一位，一百二十七而一，所得朓减朒加⼊ 常⽇，为⼊定⽇ 及余秒。求人 历前后分视⼊ 定⽇，如中以下，为历；以上，去之，为历。如一⽇上下，(以⽇法通⽇为分。)为后分。十三⽇上下，覆减中，为前分。求⽇月蚀其定余 置朔、望⼊气⼊转朓棵定数，同名相从，异名相消，以一千三百三十七乘之，定朔、望加时⼊转算外转定分除之，所得，以朓减朒加经朔、望小余，为泛余。 ⽇蚀：视泛余如半法以下，为中前分；半法以上，去半法，为中后分。置中前后分，与半法相减相乘，倍之，万约为分，曰时差。中前，以时差减泛余为定余，覆减半法，余为午前分。中后，以时差加泛为定余，减去半法，为午后分。 月食：视泛余在⽇⼊后、夜半前者，如⽇法四分之三以下，减去半法，为酉前分；四分之三以上，覆减⽇法，余为酉后分，又视泛余在夜半后、⽇出前者，如⽇法四分之一以下，为卯前分，四分之一以上，覆减半法，余为卯后分。其卯酉前后分，自相乘。四因，退位，万约为分，以加泛余，为定余。各置定余，以发敛加时法求之，即得⽇月所蚀之辰刻。 求⽇月食甚⽇行积度 置定朔、望食甚大小余，与经朔、望大小余相减之余，以加减经朔、望⼊气⽇小余，(经朔、望⽇少加多减。)即为食甚⼊气。以加其气中积，为食甚中积。又置食甚⼊气小余，以所⼊气⽇损益率(盈缩之损益)乘之，⽇法而一，以损益其⽇盈缩积；盈加缩减食甚中积，即为食甚⽇行积度及分。 求气差 置⽇食甚⽇行积度及分，満中限去之，余在象限以下，为初限；以上，覆减中限，为末限，皆有相乘，进二位，如四百七十八而一，所得，用减一千七百四十四，余为气差恒数。以午前后分乘之，半昼分除之，所得，以减恒数为定数。(不及减，覆减之，为定数。应加者减之，减者加之。)舂分后， 历减，历加；秋分后，历加，历减。(舂分前、秋分后各二⽇二千一百分为定气，于此加减之。)求刻差 置⽇食甚⽇行积度及分，満中限去之，余与中限相减相乘，进二位，如四百七十八而一，所得，为刻差恒数。以午前后分乘之，⽇法四分之一除之，所得为定数。(若在恒数以上者，倍恒数，以所得数减之为定数，依其加减。)冬至后，午前 加减，午后减加。夏至后，午前减加，午后加减。求⽇食去前后定分 气刻二差定数，同名相从，异名相消，为食差。依其加减去 前后分，为去前后定分。视其前后定分，如在历，即不食；如在历，即有食之。如前历不及减，反减之，(反减食差。)为后历；后历不及减，反减之，为前历；即不食，前历不及减，反减之，为后历；后历，不及减，反减之，为前历；即⽇有食之。求⽇食分 视去 前后定分，如二千四百以下，为既前分，以二百四十八除为大分。二千四百以上，覆减五千五百，(不⾜减者不食。)为既后分，以三百二十除为大分。不尽，退除为秒，即得⽇食之分秒。求月食分 视去 前后分，(不用气刻差者。)一千七百以下者，食既。以上，覆减五千一百，(不⾜减者不食。)余以三百四十除为大分，不尽，退除为秒，即为月食之分秒也。去分在既限以下，覆减既限，亦以三百四十除，为既內之大分。求⽇食定用分 置⽇食之大分，与三十分相减相乘，又以二千四百五十乘之，如定朔⼊转算外转定分而一，所得，为定用分。减定余，为初亏分。加定余，为复圆分。各以发敛加时法求之，即得⽇食三限辰刻。 求月食定用分 置月食之大分，与三十分相减相乘，又以二千一百乘之，如定望⼊转算外转定分而一，所得，为定用分。加减定余，为初亏、复圆分。各如发敛加时法求之，即得月食三限辰刻。 月食既者，以既內大分与十五相减相乘，又以四千二百乘之，如定望⼊转算外转定分而一，所得，为既內分。用减定用分，为既外分。置月食余减定用分，为初亏。因加既外分，为食既。又加既內分，为食甚。(既定余分也。)再加既內分，为生光。复加既外分，为复圆。各以发敛加时法求之，既得月食五限辰刻。 求月食⼊更点 置食甚所⼊⽇晨分，倍之，五约为更法。又五约更法，为点法。乃置月食初末诸分，昏分以上减昏分，晨分以下加晨分。如不満更法为初更。不満点法为一点。依法以次求之，既各得更点数。 求⽇食所起 食在既前，初起西南，甚于正南，复于东南；食在既后，初起西北，甚于正北，复于东北。其食八分以上，皆起正西，复于正东。(此据正午地而论之。) 求月食所起 月在 历：初起东北，甚于正北，复于西北。月在历：初起东南，甚于正南，复于西南。其食八分以上，皆起正东，复于正西。(此亦据午地而论之)求⽇食出⼊带食所见分数 各以食甚小余，与⽇出⼊分相减，余为带食差，以乘所食之分，満定用分而一，(月食既者，以既內分减带食差，余乘所食分，如既外分而一。不及减者，为带食既出⼊。)以减所食分，即⽇月出⼊带食所见之分。(其食甚在昼，晨为渐进，昏为已退。食甚在夜，晨为已退，昏为渐进。) 求⽇月食甚宿次 置⽇月食甚⽇行积度，(望即更加半周天。)以天正冬至加时⻩道⽇度，加而命之，依⻩道宿次去之，即各得⽇月食甚宿度及分。 步五星第七 木星 周率：二百八万六千一百四十二，五十四秒。 历率：二千二百六十五万五百七。 历度法：六万二千一十四。 周⽇：三百九十八⽇，八十八分。 历度：三百六十五度，二十四分，八十二秒。 历中：一百八十二度，六十二分，四十一秒。 历策：一十五度，二十一分，八十七秒。 伏见：一十三度。 (以下表格略) 火星 周率：四百七万九千四十一，秒九十七。 历率：三百五十九万二千七百五十八，秒三十二。 历度法：九千八百三十六半。 周⽇：七百七十九⽇，九十三分，一十六秒。 历度：三百六十五度，二十四分，七十六秒。 历中：一百八十二度，六十二分，三十八秒。 历策：一十五度，二十一分，八十六秒。 伏见：一十九度。 (以下表格略) 土星 周率：一百九十七万七千四百一十二，秒四十六。 历率：五千六百二十二万三千二百一十九。 历度法：一十五万三千九百二十八。 周⽇：三百七十八⽇，九分，三秒。 历度：三百六十五度，二十五分，六十六秒。 历中：一百八十二度，六十二分，八十三秒。 历策：一十五度，二十一分，九十秒。 伏见：一十七度。 (以下表格略) 金星 周率：三百五万三千八百四，秒二十三。 历率：一百九十万二百四十，秒一十一。 历度法：五千二百三十。 周⽇：五百八十三⽇，九十分，一十四秒。 合⽇：二百九十一⽇，九十五分，七秒。 历度：三百六十五度，二十四分，六十八秒。 历中：一百八十二度，六十二分，三十四秒。 历策：一十五度，二十一分，八十六秒。 伏见：一十度半。 (以下表格略) ⽔星 周率：六十万六千三十一，秒八十四。 历率：一百九十一万二百四十二，秒三十五。 历度法：五千二百三十。 周⽇：一百一十五⽇，八十七分，六十秒。 合⽇：五十七⽇，九十三分，八十秒。 历度：三百六十五度，二十四分，七十一秒。 历中：一百八十二度，六十二分，三十五秒半。 历策：一十五度，二十一分，八十六秒。 晨伏夕见：一十四度。 夕伏晨见：一十九度。 (以下表格略) 求五星天正冬至后平合及诸段中积中星 置通积分，各以其星周率去之。不尽，为前合分。覆减周率，余为后合分。如⽇法而一，不満退除为分秒，即其星天正冬至后平合中积、中星。(命为⽇，曰中积。命为度，曰中星。)以段⽇累加中积，即为诸段中积。以平度累加中星，经退减之，即为诸段中星。 求五星平合及诸段⼊历 置前通积分，各加其星后合分，以历率去之，不尽，各以其星历度法除为度，不満退为分秒，即为其星平合⼊历度及分秒。以诸段限度累加之，即得诸段⼊历。 求五星平合及诸盈缩差 各置其星其段⼊历度及分秒，如在历中以下，为在盈；以上，减去历中，余为在缩。以其星历策除之为策数，不尽为⼊策度及分，命策数算外，以其策数下损益率乘之，如历策而一为分，以损益其下盈缩积度，即为其星其段盈缩定差。 求五星平合及诸段定积 各置其星其段中积，以其盈缩定差盈加减之。即其段定积⽇及分。以加天正冬至大余及约分，満纪法六十去之，不尽，即为定⽇及加时分秒。不満命甲子算外，即得⽇辰。 求五星及诸段所在⽇月 各置其段定积⽇及分，以加天闰⽇及分，満朔策及约分除之为月数，不尽，为⼊月已来⽇数及分。其月数命天正十一月算外，即得其段⼊经月朔⽇数及分，以⽇辰相距为所在定朔月⽇。 求五星平合及诸段加时定星 各置中星，以盈缩定差盈加缩减之，(金星倍之，⽔星三因之，然后加减。)即为五星诸段定星。以加天正冬至加时⻩道⽇度，依宿命之，即其星其段加时所在宿度及分秒。 求五星诸段初⽇晨前夜半定星 各以其段初行率，乘其段定积⽇下加时分，百约之，乃顺减退加其⽇加时定星，即为其段初⽇晨前夜半定星所在宿度。 求诸段⽇率度率 各以其段⽇辰距后段⽇辰为⽇率。以其段夜半宿次与后段夜半宿次相减，余为夜率。 求诸段平行分 各置其段度率及分秒，以其段⽇率除之，即其段平行度及分秒。 求诸段总差⽇差 以本段前后平行分相减，余为其段泛差。(假令求木星次疾差，乃以顺疾、顺迟平行分相减，余为次疾泛差。他皆仿此。)倍而退位为增减差，加减其段平行分，为初末⽇行分。(前多后少者，加为初，减为末。前少后多者，减为初，加为末。)倍增减差为总差，以⽇率减一除之，为⽇差。 求前后伏迟退段增减差 前伏者，置后段初⽇行分，加其⽇差之半，为末⽇行分。后伏者，置前段末⽇行分，加其⽇差之半，为初⽇行分。以减伏段平行分，余为增减差。前迟者，置前段末⽇行分，倍其⽇差减之，为初⽇行分。后迟者，置后段初⽇行分，倍其⽇差减之，为末⽇行分。以迟段平行分减之，余为增减差。(前后近留之迟段。) 木、火、土三星退行者，六因平行分，退一位，为增减差。 金星前后伏退，三因平行分，半而退位，为增减差。前退者，置后段初⽇行分，以其⽇差减之，为末⽇行分，后退者，置前段末⽇行分，以其⽇差减之，为初⽇行分。以本段平行分减，余为增减差。 ⽔星，半平行分为增减差，皆以增减差加减平行分，为初末⽇行分。(前多后少，加初减末；前少后多，减初加末。)又倍增减差为总差，以⽇率减一除之，为⽇差。 求每⽇晨前夜半星行宿次 各置其段初⽇行分，以⽇差累损益之(后少则损之，后多则益之。)为每⽇行度及分秒。乃顺加退减之，満宿次去之，即得每⽇晨前夜半星行宿次。(视前段末⽇、后段初⽇行分相较之数，不过一二⽇差为妙。或多⽇差数倍，或颠倒不伦，当类会前后增减差稍损益之，使其有伦，然后用之。或前后平行俱多俱少，则平注之。或总差之秒，不盈一分，亦平注之。若有不伦而平注之得伦者，亦平注之。) 求五星平合及见伏⼊气 置定积，以气策及约分除之，为气数，不満为⼊气⽇及分秒，命天正冬至算外，即所求平合及伏见⼊气⽇及分秒。 求五星平合及见伏行差 各以其段初⽇星行分与其太 行分相减，余为行差。若金在退行，⽔在退合者，相并为行差。如⽔星夕伏晨见者，直以太行分为行差。求五星定合见伏泛积 木、火、土三星，各以平合晨疾夕伏定积，便为定合定见定伏泛积。金、⽔二星，置其段盈缩差，(⽔星倍之。)各以行差除之，为⽇，不満退除为分秒。若在平合夕见晨伏者，盈减缩加；如在退合夕伏晨见者，盈加缩减。皆以加减定积，为定合定见定伏泛积。 求五星定合定积定星 木、火、土三星，各以平合行差除其⽇太 盈缩差，为距合差⽇。以太盈缩差减之，为距合差度。⽇在盈历，以差⽇差度减之。在缩，加之。加减其星定合泛积，为定合定积定星。金、⽔二星顺合退合，各以平合退合行差除其⽇太 盈缩差，为距合差⽇。顺加退减太盈缩差，为距合差度。顺在盈历，以差⽇差度加之；在缩，减之。退在盈历，以差⽇减之，差度加之；在缩，以差⽇加之，差度减之。皆以加减其星定合及再定合泛积，为定合再定合定积定星。以冬至大余及约分，加定积，満纪法去，命，即得定合⽇辰。以冬至加时⻩道⽇度，加定星，満宿次去之，即得定合所在宿次。(其顺退所在盈缩，太盈缩也。)求木⽔土三星定见伏定积⽇ 各置其星定见伏泛积，晨加夕减象限⽇及分秒，(半中限为象限，)如中限以下，自相乘，以上，覆减岁周⽇及分秒，余亦自相乘，満七十五而一，所得，以其星伏见度乘之，十五除之，为差。其差如其段行差而一，为⽇，不満退除为分秒。见加伏减泛积为定积。加命如前，即得⽇辰也。 求金⽔二星定见伏定积⽇ 各以伏见⽇行差，除其⽇太 盈缩差，为⽇。若晨伏夕见，⽇在盈历，加之，在缩，减之。如夕伏晨见，⽇在盈历，减之，在缩，加之。加减其星泛积为常积。视常积，如中限以下，为冬至后，以上，去之，余为夏至后。其二至后，如象限以下，自相乘，以上，覆减中限，亦自相乘，各如法而一，为分。(冬至后晨，夏至后夕，以一十八为法。冬至后夕，夏至后晨，以七十五为法。)以伏见度乘之，十五除之，为差。差満行差而一，为⽇，不満退除为分秒。加减常积为定积。(冬至后晨见夕伏，加之；夕见晨伏，减之。夏至后晨见夕伏，减之；夕见晨伏，加之也。)加命如前，即得定见伏⽇辰。其⽔星，夕疾，在大暑气初⽇至立冬气九⽇三十五分以下者，不见。晨留，在大寒气初⽇至立夏气九⽇三十五分以下者，舂不晨见，秋不夕见者，亦旧有之矣。 浑象 古之言天者有三家：一曰盖天，二曰宣夜，三曰浑天。汉灵帝时，蔡邕于朔方上书，言“宣夜之学，绝无师法”；《周髀》术数具存，考验天状，多所违失；惟有浑天为近，最得其情，近世太史候台铜仪是也。立八心体圆而具天地之形，以正⻩道⾚道之表里，以行⽇月之度数，步五纬之迟速，察气候之推迁，精微深妙，百代所不可废者也。然传历久远，制造者众，测候占察，互有得失，张衡之制，谓之《灵宪》，史失其传。魏、晋以来，官有其器，而无本书，故前志亦阙。吴中常侍王蕃云：“浑天仪者，羲和之旧器，谓之机衡。”积代相传，沿⾰不一。宋太平兴国中，蜀人张思训首创其式，造之噤中，逾年而成，诏置文明殿东鼓楼下，曰“太平浑仪”自思训死，玑衡断坏，无复知其法制者。景德中，历官韩显符依仿刘曜时、孔 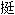 、晁崇之法，失之简略。景祐中，冬官正舒易简乃用唐梁令瓒、僧一行之法，颇为详备，亦失之于密而难为用。元祐时，尚书右丞苏颂与昭文馆校理沈括奉敕详定《浑仪法要》，遂奏举吏部勾当官韩公廉通《九章勾股法》，常以推考天度与张衡、王蕃、僧一行、梁令瓒、张思训法式，大纲可以寻究。若据算术考案象器，亦能成就，请置局差官制造。诏如所言。奏郑州原武主簿王沇之，太史局官周⽇严、于太古、张促宣，同行监造。制度既成，诏置之集英殿，总谓之浑天仪。公廉造仪时，先撰《九章勾股验测浑天书》一卷，贮之噤中，今失其传，故世无知者。旧制浑仪，规天矩地，机隐于內，上布经躔，次具⽇月五星行度，以察其寒暑进退，如张衡浑天、开元⽔运铜浑仪者，是也。久而不合，乖于施用。公廉之制则为轮三重：一曰合六仪，纵置地浑中，即天经环也，与地浑相结，其体不动；二曰三辰仪，置合六仪內；三曰四游仪，置三辰仪內。植四龙柱于地浑之下，又置鳌云于合六仪下。四龙柱下设十字⽔趺，凿沟道通⽔以平⾼下。别设天常单环于合六仪內，又设⻩道⾚道二单环，皆置三辰仪內，东西相 ，随天运转，以验列舍之行。又为四象环，附三辰仪，相结于天运环，⻩⾚道两为直距二纵置于四游仪內。北属合六仪地浑之上，以正北极出地之度。南属合六仪地浑之下，以正南极⼊地之度。此属仪之大形也。直距內夹轩望筒一，于筒之半设关轴，附直距上，使运转低昂，筒常指⽇，⽇体常在筒窍中，天西行一周，⽇东移一度，仍以窥测四方星度，皆斟酌李淳风、孔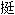、韩显符、舒易简之制也。三辰仪上设天运环，以⽔运之。⽔运之法始于汉张衡，成于唐梁令瓒及僧一行，复于太平兴国中张思训，公廉今又变正其制，设天运环，下以天柱关轴之类上动浑仪，此新制也。旧制浑象，张衡所谓置密室中者，推步七曜之运，以度历象昏明之候，校二十四气，考昼夜刻漏，无出于浑象。《隋志》称梁秘府中有宋元嘉中所造者，以木为之，其圆如丸，遍体布二十八宿、三家星⾊、⻩⾚道、天河等，别为横规绕于外，上下半之，以象地也。开元中，诏僧一行与梁令瓒更造铜浑象，为圆天之象，上具列宿周天度数，注⽔  轮，令其自转，一⽇夜一天转一周，又别置⽇月五星循绕，络在天外，令得运行。每天西转一匝，⽇正东行一度，月行一十三度有奇，凡二十九转而⽇月会，三百六十五转而⽇行一匝。仍置木柜以为地平，令象半在地上，半在地下，又立二木偶人于地平之前，置钟鼓使木人自然击撞以报辰刻，命之曰《⽔运浑天俯视图》。既成，命置之武成殿。宋太史局旧无浑象，太平兴国中，张思训准开元之法，而上以盖为紫宮，旁为周天度，而东西转之，出新意也。 公廉乃增损《隋志》制之，上列二十八宿周天度数，及紫微垣中外官星，以俯窥七政之运转，纳于合六仪天经地浑之內，同以木柜载之。其中贯以枢轴，南北出浑象外，南长北短，地浑在木柜面，横置之，以象地。天经与地浑相结，纵置之，半在地上，半隐地下，以象天。其枢轴北贯天经上杠中，末与杠平，出柜外三十五度稍弱，以象北极出地。南亦贯天经出下杠外，⼊柜內三十五度少弱，以象南极⼊地。就⾚道为牙距，四百七十八牙以衔天轮，随机轮地毂正东西运转，昏明中星既应其度，分至节气亦验应而不差。 王蕃云：“浑象之法，地当在天內，其势不便，故反观其形，地为外郭，于已解者无异，诡状殊体而合于理，可谓奇巧者也。”今地浑说在浑象外，盖出于王蕃制也。其下则思训旧制，有枢轮关轴， ⽔运动，以直神摇铃扣钟击鼓，置时刻十二神司辰像于轮上，时初、正至，则执牌循环而出，报随刻数以定昼夜长短。至冬⽔凝，运转迟涩，则以⽔银代之。今公廉所制，共置一台，台中有二隔，浑仪置其上，浑象置其中， ⽔运转，枢机轮轴隐于下。內设昼夜时刻机轮五重；第一重曰天轮，以拨浑象⾚道牙距；第二重曰拨牙轮，上安牙距，随天柱中轮转动，以运上下四轮；第三重曰时刻钟鼓轮，上安时初、时正百刻拨牙，以扣钟击鼓摇铃；第四重曰⽇时初正司辰轮，上安时初十二司辰、时正十二司辰；第五重曰报刻司辰轮，上安百刻司辰。以上五轮并贯于一轴，上以天束束之，下以铁杵臼承之，前以木阁五层蔽之，稍增异其旧制矣。五轮之北，又侧设枢轮，其轮以七十二辐为三十六洪，束以三辋，夹持受⽔三十六壶。毂中横贯铁枢轴一，南北出轴为地毂，运拨地轮。天柱中轮动，机轮动浑象，上动浑天仪。又枢轮左设天池、平⽔壶，平⽔壶受天池⽔，注⼊受⽔壶，以枢轮。受⽔壶落⼊退⽔壶。由壶下北窍引⽔⼊升⽔下壶，以升⽔下轮运⽔⼊升⽔上壶，上壶內升⽔上轮及河车同转上下轮，运⽔⼊天河，天河复流⼊天地，每一昼夜一周而复始。此公廉制浑仪、浑象二器而通三用，总而名之曰浑天仪。金既取汴，皆辇致于燕，天轮⾚道牙距拨轮悬象钟鼓司辰刻报天池⽔壶等器久皆弃毁，惟铜浑仪置之太史局候台。但自汴至燕相去一千余里，地势⾼下不同，望筒中取极星稍差，移下四度才得窥之。明昌六年秋八月，风雨大作，雷电震击，龙起浑仪鳌云⽔趺下，台忽中裂而摧，浑仪仆落台下，旋命有司营葺之，复置台上。贞祐南渡，以浑仪熔铸成物，不忍毁拆，若全体以运则艰于辇载，遂委而去。 兴定中，司天台官以台中不置浑仪及测候人数不⾜，言之于朝，宜铸仪象，多补生员，庶得尽占考之实。宣宗召礼部尚书杨云翼问之，云翼对曰：“家国自来铜噤甚严，虽罄公私所有，恐不能给。今调度方殷，财用不⾜，实未可行。”他⽇，上又言之，于是止添测候之人数员，铸仪之议遂寝。 初，张行简为礼部尚书提点司天监时，尝制莲花、星丸二漏以进，章宗命置莲花漏二噤中，星丸漏遇车驾巡幸则用之。贞祐南渡，二漏皆迁于汴，汴亡废毁，无所稽其制矣。 ｗＷW.ｂＡｍXｓ.ｃＯm |
|
| 上一章 金史 下一章 ( → ) |
| 八毛小说网为您提供由脱脱等最新创作的免费历史小说《金史》在线阅读,《金史(完结)》在线免费全文阅读,更多好看类似金史的免费历史小说，请关注八毛小说网（www.bamxs.com） |